32.14 Latin Hypercube Sampling

Latin Hypercube Sampling (LHS) is a statistical method for generating a near-random sample of parameter values from a multidimensional distribution. Within TreeAge Pro, we apply this to all sampled distributions that together represent a multi-dimensional parameter space.

By default, TreeAge Pro draws samples from each distribution independently, which is typically appropriate. However, if you have a large number of distributions and/or long analyses, Latin Hypercube Sampling can generate a set of samples that represent the overall parameter set with fewer PSA model calculations. You might choose to use this option if your PSA analysis is taking a long time and you want to try running it with fewer iterations.

How does Latin Hypercube Sampling work?

Latin Hypercube Sampling (LHS) divides the distribution parameter space into multi-dimensional "hypercubes" and generates samples such that each dimension of a hypercube is only used once. This prevents very similar samples from being drawn from any single distribution. In theory, LHS can generate a set of samples that represents the overall parameter space with fewer actual sample sets.

To better understand this concept, let's examine example model Latin Hypercube Sampling.trex and run some analyses. The first strategy samples two uniform distributions that only return integers between 1 and 8. Limiting these distributions to integers highlights that each sampled value will not be repeated when using LHS.

If we run PSA with 8 iterations on the first strategy without LHS, the distributions will be sampled independently. The CE scatterplot below illustrates these samples with one distribution for "cost" y-axis and the other for "effectiveness" x-axis.

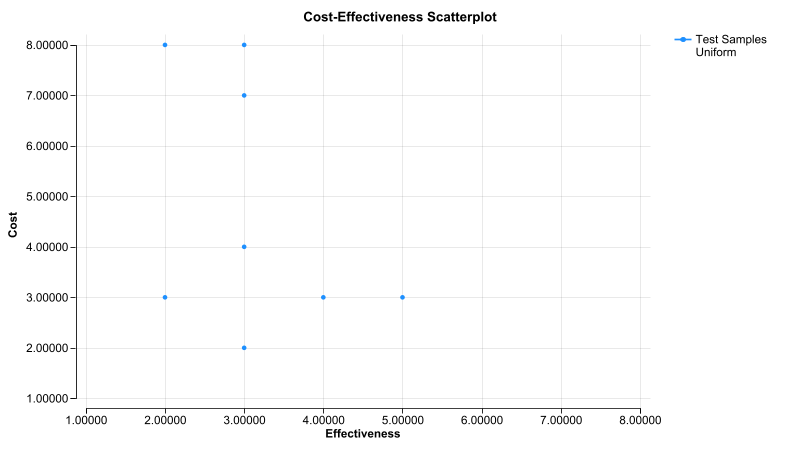
Note that for each distribution, several values were sampled more than once. For example, on the x-axis, distribution Uniform_X generated the value 3 four times. There are also repeated sampled values from the Uniform_Y distribution. In this analysis, the repeat samples are especially apparent since there are only 8 distinct possible samples from each distribution.

Latin Hypercube Sampling restricts sampling to avoid previously drawn samples within the overall hypercube. Now let's run the same analysis with Latin Hypercube Sampling through Tree Preferences > Monte Carlo Options > Distribution Sampling as shown below.

When we run the same analysis and graph with LHS, we get unique samples from each distribution because previously used samples are avoided.

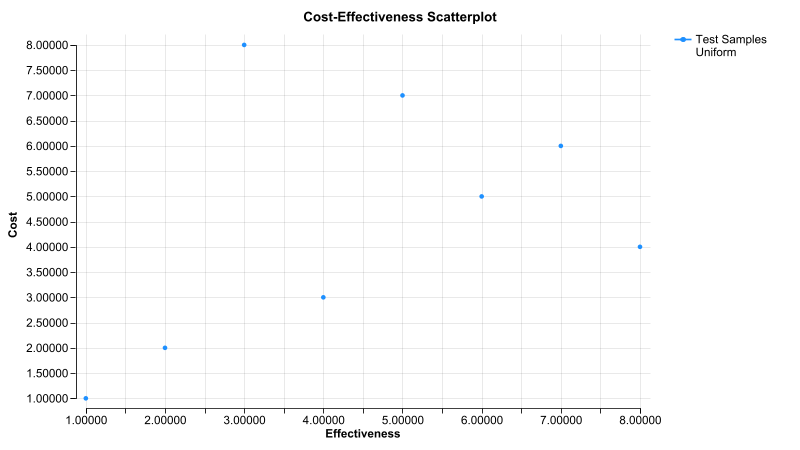
LHS was able to better represent the full parameter space with 8 total samples that clearly was not achieved without LHS.

The example above is an extreme example of LHS because there were 8 samples in the analysis and there were only 8 possible values to sample from each distribution. Let's look at a more general example using the second strategy with two normal distributions. For these analyses, we will run 100 samples with and without LHS sampling.

Note that normal distributions are continuous, so the total parameter space for each distribution is divided into 100 intervals based on the number of samples drawn. No two samples from any distribution will be drawn from the same interval in multiple dimensions.

Without LHS, you see some bunching of values vertically and horizontally.

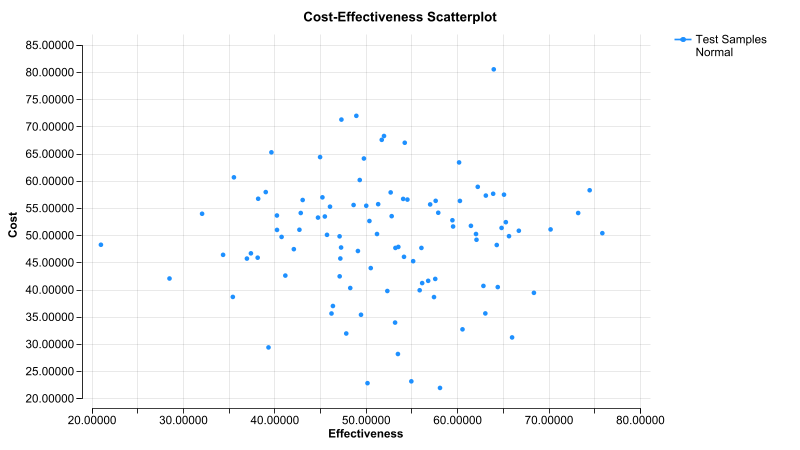
With LHS, there is less bunching because each sampled value "hypercube" in the graph does not allow repeated values either vertically or horizontally. Note this is less obvious when the samples are within a continuous range because the dimensions of the cube are ranges of values.

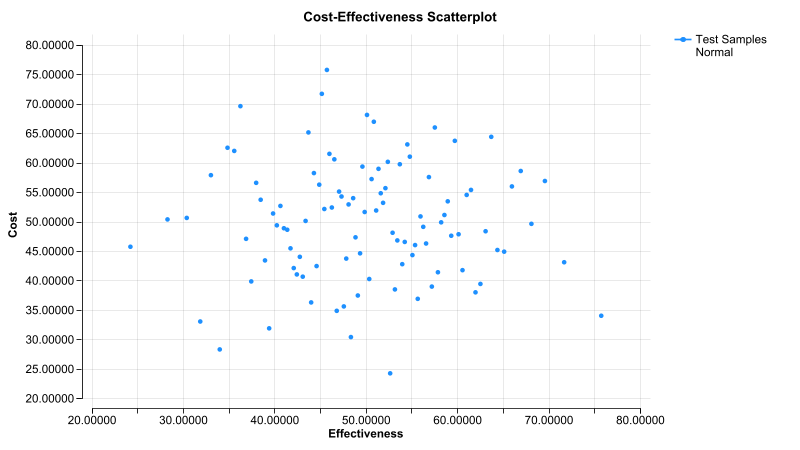
Note that we have presented these results in 2 dimensions for visualization, but the hypercube will be N-dimensional based on the number of distributions sampled.

Typically, LHS sampling would be applied using each distribution's native shape. The "use uniform shape" option equally distributes values within the 95% confidence interval rather than following the shape of the distribution (where normal distribution samples will tend to be close to the mean).