35.3 Converting Distributions to Transition Probabilities - DistTransProb
The function DistTransProb converts time-to-event distributions to Markov transition probabilities for any time period.
Survival Analysis may determine that an event occurs within a patient population based on a time-to-event distribution. For example, time to progression may occur based on a Weibull distribution. This data can be used in both DES and Markov models, but in different ways.
-
DES: In a DES model, the time-to-event distribution would be sampled directly to get a new event time for each patient in the model.
-
Markov: In a Markov model, you can derive transition probabilities for the event from the underlying time-to-event distribution.
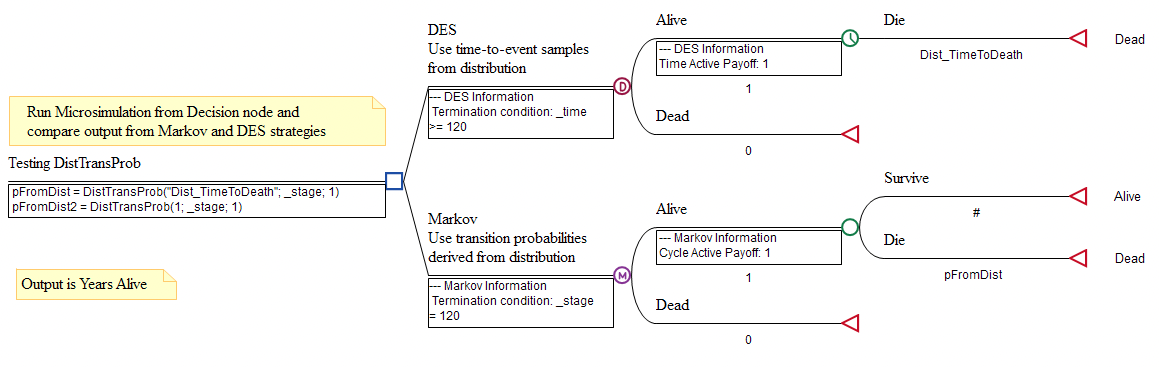
To demonstrate the equivalence of the time-to-event distribution with DES (sampling) vs. Markov (derived transition probabilities), consider the Healthcare tutorial example model DistTransProb vs DES.trex.
The time-to-event distribution Dist_TimeToDeath is a Weibull distribution, which is commonly used for time-to-event distributions.
In the DES model strategy, the Dist_TimeToDeath distribution is used directly in the time expression for death. Each patient will get a different time for death sampled from the distribution.
In the Markov model, the Dist_TimeToDeath distribution is converted to the appropriate probability of death for each cycle using the DistTransProb function.
There are two possible syntax options for the DistTransProb function presented below - referencing the distribution by name or by index. Both are in the model for reference, but only the first is used.
-
pFromDist = DistTransProb("Dist_TimeToDeath"; _stage; 1)
-
pFromDist2 = DistTransProb(1; _stage; 1)
More generically, the two function call options are described below.
-
DistTransProb("distribution name in quotes"; cycle_time_start ; cycle_time_length)
-
DistTransProb(distribution_index; cycle_time_start ; cycle_time_length)
The arguments represent the following:
-
distribution reference: a reference to the appropriate time-to-event distribution within the model - either by name in quotes or by index without quotes;
-
cycle_time_start: the start time for each cycle; and
-
cycle_time_length: the length of the Markov cycle (see below for more details about this argument).
Note that the second and third arguments reflect the specific time period for which you are calculating the probability for the underlying distribution. The argument values depend on the time relationship between the time-to-event distribution and the Markov cycle length. Let's consider some examples.
-
Time-to-event distribution is in years, and the Markov cycle length is also in years.
-
The two time periods are consistent, so one cycle (_stage) is equivalent to the one time unit from the underlying distribution.
-
Syntax: DistTransProb("distribution_name"; _stage; 1)
-
-
Time-to-event distribution is in months, and the Markov cycle length is also in months.
-
The two time periods are consistent, so one cycle (_stage) is equivalent to the one time unit from the underlying distribution.
-
Syntax: DistTransProb("distribution_name"; _stage; 1)
-
-
Time-to-event distribution is in years, but the Markov cycle length is in months.
-
The two time periods are not consistent, so one cycle (_stage) is only 1/12 of a time unit from the underlying distribution.
-
Syntax: DistTransProb("distribution_name"; _stage/12; 1/12)
-
Refer to the Healthcare tutorial example model DistTransProb vs DES Cycle Length.trex for syntax examples.
We can run microsimulation on the model DistTransProb vs DES.trex, and the output will show almost indentical values for the Markov and DES "strategies" of the model. The output is the average life years and this shows, on average, the same results will be returned from a sample from the Weibull Distribution or from the Transition Probability in the Markov model.
Note that there could be a special case where the time-to-event starts later in the analysis. For example, you could have a distribution for time-to-death after progression. In such a case, the distribution time 0 is not the same as the Markov time 0 because some period of time could take place before progression.
In this situation, you would need to record the time of progression for each patient in a simulation to set a "new time 0" point for the time-to-death distribution.
-
Store time of progression in tracker: t_time_prog.
-
Time of death post progression is: DistTransProb( "dist_name"; (_stage-t_time_prog); 1)
Note that the above would change if the time periods for the distribution and Markov cycle were not consistent.
Distributions with special inputs
There are some distributions which need some special consideration when using DistTransProb.
For a Multivariate distribution, an additional argument can be used:
-
DistTransProb ("distribution_name"; variate; time_cycle_start ; time_cycle_length)
-
DistTransProb (index_of_distribution; variate; time_cycle_start ; time_cycle_length)
For LogNormal and LogLogistics distributions, using DistTransProb can create an error if the first value to be sampled is at _stage = 0, because Log(0) is undefined.
-
There will be an error when _stage = 0 if you use: DistTransProb("dist_from_log";_stage; time_cycle_length).
-
Define instead the probability as:
-
transition_prob = if(_stage = 0; DistTransProb("dsurvival"; _stage + 1e-9; 12) ; DistTransProb("dsurvival"; _stage; 12))
-
This ensures that when _stage = 0 the is a small constant added "1e-9" to the _stage, allowing the first cycle (_stage = 0) to run without the error. You can use even smaller values "1e-12", and compare if there is a material change to the transition_prob dependent on the small constant.
